[백준 BOJ 21213] Mentors | 퍼피가 PS하는 블로그

https://www.acmicpc.net/problem/21213

21213번: Mentors

문제 요약

번호가 $1$부터 $N$까지 부여된 $N$개의 노드를 갖는 트리가 있다. 각 노드는 많아야 2개의 자식을 가질 수 있으며, 모든 자식의 번호는 노드보다 작아야 한다. $R$번 노드를 리프로 갖는 트리의 개수를 $M$으로 나눈 나머지를 구하여라.

 

풀이

핵심 아이디어는 전체에서 $R$번이 리프가 아닌 경우를 빼 주는 것입니다.

 

먼저 전체 경우의 수를 구하기 위해 노드가 N개인 트리의 수를 $DP[N]$이라 합시다.

$N-1$번 노드는 $N$번 노드만을 부모로 가질 수 있습니다. 따라서 $N$번이 루트, $N-1$번은 그 자식입니다.

이때 $N$번 노드는 $N-1$번 노드만 자식으로 가질 수도 있고, $N-1$번 외에 다른 노드를 추가로 자식으로 가질 수도 있습니다. 경우를 나눠 봅시다.

 

1) $N$번 노드가 $N-1$번 노드만을 자식으로 가지는 경우

$N-1$번 노드를 루트로 하는 트리의 개수를 구하는 문제가 되므로 $DP[N-1]$

 

2) $N$번 노드가 $N-1$번 노드와 $i(1 \leq i \leq N-2$)번 노드를 동시에 자식으로 가지는 경우

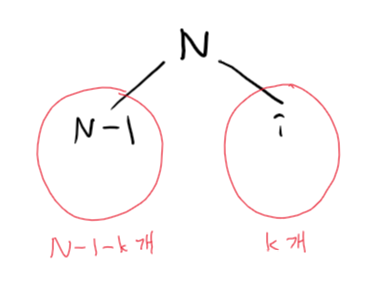
$i$번 노드를 루트로 하는 서브트리의 노드 개수를 $k$개라 하면, $N-1$번 노드를 루트로 하는 서브트리에는 $N-1-k$개의 노드가 있음을 알 수 있습니다.

우선 이렇게 $k$개를 선택하는 경우의 수는 $i$보다 작은 번호의 노드들 중 $k-1$개를 선택하는 방법의 수인 $\binom{i-1}{k-1}$입니다.

이렇게 각 서브트리에 들어갈 노드가 정한 후 노드를 배치하면 되므로 이 경우의 수는 $DP[N-1-k]*DP[k]$입니다.

따라서 경우의 수는 $\sum_{k=1}^{i}\binom{i-1}{k-1}DP[k]DP[N-1-k]$입니다. i가 1부터 N-2까지 가능하므로

 

$DP[N]=DP[N-1]+\sum_{i=1}^{N-2}\sum_{k=1}^{i}\binom{i-1}{k-1}DP[k]DP[N-1-k]$

$=DP[N-1]+\sum_{k=1}^{N-2}\sum_{i=k}^{N-2}\binom{i-1}{k-1}DP[k]DP[N-1-k]$

$=DP[N-1]+\sum_{k=1}^{N-2}\binom{N-2}{k-1}DP[k]DP[N-1-k]$

 

이 됩니다. 위 식은 하나당 $O(N)$의 시간복잡도에 계산할 수 있으므로 총 시간복잡도 $O(N^2)$에 계산 가능합니다.

 

다음으로 $R$이 리프가 아닌 경우의 수를 구해봅시다. $R$이 리프이며 $N$개의 노드를 갖는 트리의 가짓수를 $f(N, R)$로 둡시다.

$N$개의 노드를 갖는 트리에서, $R$을 루트로 하는 서브트리의 노드의 수를 $k$로 둡시다. $f(N, R)$은 $k=1$일 떄 경우의 수이며, 우리는 $k=2, ..., R$인 경우를 구해 전체에서 빼 줍시다.

기존의 트리에서 $R$을 제외한 $k-1$개의 노드를 제거한 트리에서는 $R$이 리프가 됩니다.

이 과정에서 $R$보다 번호가 작은 $k-1$개의 노드를 제거했기 때문에 $R$의 번호는 아래에서 $R-(k-1)$번째가 되고, 총노드의 수는 $N-(k-1)$개이므로 이때 트리의 개수는 $f(N-k+1, R-k+1)$이 됩니다.

$k-1$개의 노드를 $R$ 밑에 배열하는 경우의 수는 노드가 $k$개인 트리의 개수 $DP[k]$입니다.

일정한 $k$에 대해 총 경우의 수는 $f(N-k+1, R-k+1)*DP[k]$에, $R$보다 작은 $R-1$개의 노드 중 $k-1$개를 선택하는 방법의 수 $\binom{R-1}{k-1}$을 곱한 값입니다.

$k=2, ..., R$에서의 이 값들을 $DP[N]$에서 빼면 $f(N, R)$을 구할 수 있으므로 다음과 같은 식을 얻을 수 있습니다.

$f(N, R)=DP[N]-\sum_{k=2}^{R}f(N-k+1, R-k+1)DP[k]\binom{R-1}{k-1}$

 

거의 다 왔습니다. 이제 하나의 관찰을 해 봅시다.

위 식에서 참조되는 $f$에 대해 $N-R=(N-k+1)-(R-k+1)$이므로 $N-R$값은 일정합니다.

따라서 우리는 모든 $(N, R)$이 아니라 $N-R$값이 일정한 $R$개의 값들만 구해주면 됩니다.

 

$arr[x] = f(x+N-R, x)$라 하면, $arr[x] = DP[x+N-R] - \sum_{k=2}^{x}arr[x-k+1]DP[k]\binom{x-1}{k-1}$입니다.

정답은 $f(N, R)=arr[R]$이 됩니다.

위 식을 $O(N)$에 계산할 수 있으므로 총 시간복잡도는 $O(NR)$입니다.

따라서 모든 과정의 최종 시간복잡도는 $O(N^2)$이 됩니다.

 

Time Complexity

$O(N^2)$

 

Code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int nCr[2050][2050], visited[2050][2050];
int R, N, M;
int dp[2050], arr[2050];
int C(int n, int r)
{
    if(visited[n][r]) return nCr[n][r];
    visited[n][r] = 1;
    if(r==0||r==n) return nCr[n][r]=1%M;
    return nCr[n][r]=(C(n-1, r-1)+C(n-1, r))%M;
}
signed main()
{
    cin>>R>>N>>M;
    dp[0] = dp[1] = dp[2] = 1;
    for(int i=3;i<=N;i++){
        dp[i] = dp[i-1];
        for(int j=1;j<=i-2;j++){
            dp[i] = (dp[i] + ((dp[i-1-j]*dp[j])%M)*C(i-2, j-1)) % M;
        }
    }
    arr[1] = dp[N-R+1];
    for(int i=2;i<=R;i++){
        arr[i] = dp[i+N-R];
        for(int k=2;k<=i;k++){
            arr[i] = (arr[i] - ((C(i-1, k-1)*dp[k])%M)*arr[i-k+1])%M;
        }
        arr[i] = (arr[i] + M) % M;
    }
    cout<<arr[R]<<'\n';
}